ベクトルとあたり判定

基本公式

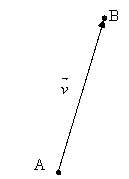ベクトルの基本の式。

　　

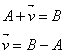
足し算、引き算はそれぞれの要素を足す。

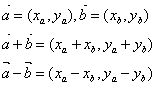
絶対値はベクトルの長さを表す。

内積・外積の式

内積
外積

内積は交換法則が成り立つが、外積は成り立たない。

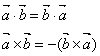
内積・外積は何を示すか

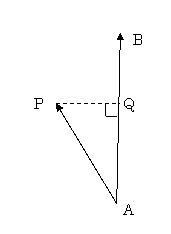
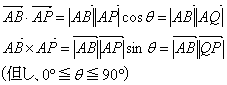
内積とはABの方向にどれだけ進んでいるか。

外積とはABとどれだけ離れているかを表す。

特にABの長さが1ならば、直接の距離を表す。

内積はABとAPが直角なら0、ABの逆方向なら負になる。

外積は、点Pが直線ABの左にあれば正、右にあれば負になる。

外積が0ならば、点Pが直線AB上にあることを示す。

（右、左の表現はxは右が正、yは上が正の時である。）

直線と点の距離

直線ABと点Pの距離＝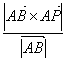

線分の交差判定

線分ABと線分CDが交差するかは、四角形ACBDが凸型四角形かどうかで判断する。

点A、点B、点C、点Dが同一直線状にある時、外積がすべて0となる。

このとき、ABを対角頂点とした矩形とCDを対角頂点とした矩形で判定する必要がある。

直線の交点

直線ABと直線CDの交点をPとすると

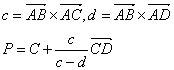
A

凸型多角形の内包判定

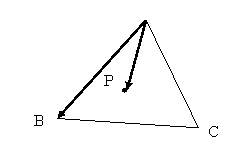
三角形ABCと点Pがあるとき以下の条件を満たすと

点Pは三角形ABCの内部にある。

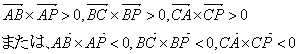
多角形の周り方向

最もxが小さく、その中でyが小さい頂点を選ぶ。

その点をCとすると、

	時計回り
	反時計回り

紐と杭のあたり判定

データの持ち方

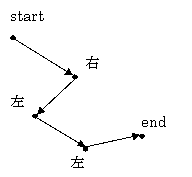杭ごとのノードを持ち、右引っ掛かり、左引っかかりを管理する。

外積を使い、次の点が右、左のどちらにあるか調べればよい。

直線状にある場合は、引っ掛かっているものとみなす。

判定は、引っ掛かり判定→外れ判定の順で行う。

以下、終点が動いた場合の引っ掛かり判定、外れ判定を解説する。

引っ掛かり判定

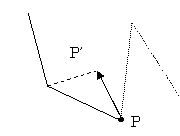
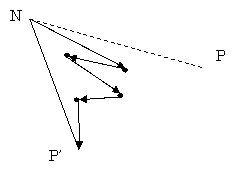
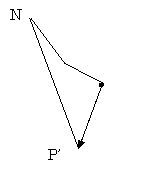
移動元P、移動先P’、最近ノードNの三角形の内部に

引っ掛かりポイントがある場合、それに引っかかるとみなす。

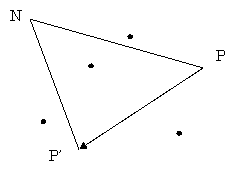
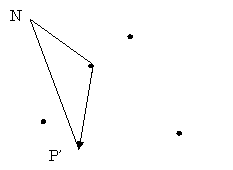
引っ掛かりポイントが複数ある場合は、線が交差しないようにひっかける。

その後、逆引っ掛かりポイントを外す。

線を交差しないように点を取る方法としては、

直線NPに近い順で、同じならNと近い順という方法を使う。

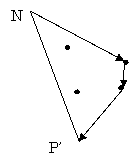
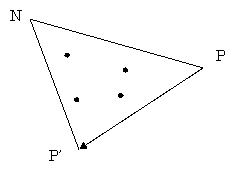
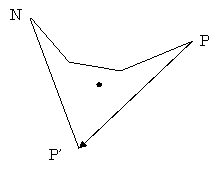
外れ判定

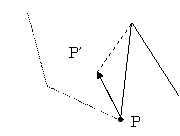
外れ判定は、ノードに割り当てられた向きと逆に引っ掛かっているかチェックする。

以下の場合、△MPP’に関しては、引っ掛かり判定でチェックしているので、

外れ判定が成立した後、MがP’に移動したものとして引っ掛かりチェックを行う。

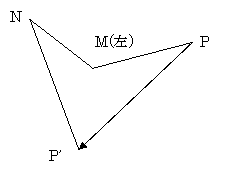
外れ判定が発生したら、それによる引っ掛かり判定を行った後、

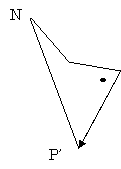
さらに外れ判定をさかのぼって行う。

途中の点が動いた時の判定

途中の点が動いた場合、その移動によって移動した点が外れてしまう場合は、

次のノードに移動したものとして引っ掛かり判定/外れ判定を行う。

　

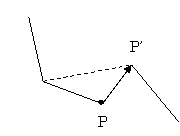
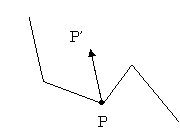
移動によって外れない場合は、ロープ全体を2つにわけ、それぞれに対して判定を行う。

＝

＋